Жай дифференциалдық теңдеулер

Жай дифференциалдық теңдеулер университеттерде, институттарда, академияларда, колледждерде оқылады. Бұл пән мектептегі математика курсына енбейді.

Бұл пән барлық жоғары оқу орындарында оқылатын жоғары математика курсының бір бөлімі, бұны оқудан бұрын математикалық анализ оқылады, оқырман осыны меңгеру үшін туынды мен интеграл сияқты ұғымдарды білу кажет.

Дифференциалдық теңдеудің аңықтамасы

Дифференциалдық теңдеу дегеніміз белгісіз функцияның туындысы бар теңдеу.

Мысалы мынандай теңдеу:

y'(x) = 2

Бұл мысалда x тең тәуелді y(x) функцияның туындысы бар.

Осы теңдеуді шешейік:

y'(x) = 2

Қандай функцияның туындысы екіге тең?

Сызықты 2x функцияның!

Осыдан y(x) = 2x

Бірақ 2x + 1, 2x + 70 және 2x - 90 функциялардың да туындылары 2 тең.

Жалпы 2x + C функциялардың туындылары 2 тең, мұндағы C тұрақты сан.

Осыдан y'(x) = 2 теңдеуінің жалпы шешімі y(x) = 2x + C.

Дифференциалдық теңдеулерге есептер

Мына дифференциалдық теңдеулерді шешіңіз:

1) y'(x) = 2x, y(x) - ?

2) y'(x) = 1/x, y(x) - ?

3) y'(x) = cos x, y(x) - ?

Жай және дербес туындылы

Дифференциалдық теңдеулер екі түрлі болады - бір айнымалыдан тәуелді және бірнеше айнымалыдан тәуелділері. Яғни белгісіз функцияның бір (жай) не бірнеше (дербес туындылы) айнымалысы бойынша туындылары бар болса.

Дербес туындылы дифференциалдық теңдеулер, бірінші курста оқылатын жоғары математика курсына енбейді, бұны арнайы математикалық физика курсында оқиды! Және тек қана физикалық және математикалық мамандықтарда.

Жоғарыдағы мысалдарда жай дифференциалдық теңдеулер көрсетілген, себебі бұларда тек бір айнымалыдан ғана тәуелді функциялар бар.

Дербес туындылы дифференциалдық теңдеулердің мысалы

Қарапайым дербес туындылы дифференциалдық теңдеу:

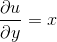
Осы теңдеуді шешейік.

Теңдеудің екі жағын y айнымалысы бойынша интегралдайық:

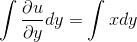
x айнымалысы теңдеудің екінші жағында параметр ретінде қарастырылады өйткені интеграл y айнымалысы бойынша алынып тұр, соңдықтан интегралдың алдына көбейткіш боп ауысады: 

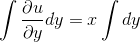
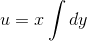
Себебі теңдеудің сол жағын y айнымалысы бойынша интегралдасақ u шығады.

Бұдан:

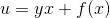
Себебі теңдеудің оң жағын y айнымалысы бойынша интегралдағанда yx және тек қана x айнымалыдан тәуелді f(x) функциясы пайда болады, мұндағы f(x) дегеніміз x айнымалысынан тәуелді кез келген функция (бұл функцияның y айнымалысы бойынша туындысы нөлге тең).

Пән: Математика

Жандос Алпысбай-ұлы